「複利」は「宇宙で最も偉大な力」

すごく大仰な見出しですね。
でもこの見出し、私が言い出した言葉ではありません。
「複利は宇宙で最も偉大な力であり、人類最大の発明とも言える」そう言ったのは、人類史上最高の頭脳の持ち主と言われる、かのアインシュタインです。
物理学の常識を次々と覆した天才物理学者をして「人類最大の発明」と言わしめたものは特殊相対性理論でもブラウン運動理論でもなく、本日このブログで解説する「複利」の力です。
資本主義社会の急成長を目の当たりにしたアインシュタインは、その原動力となる金融の力の象徴としての「複利」をそう表現したのでした。
「金利」には、大きく「単利」と「複利」の2種類があります。
両方とも金利の付き方を表す言葉ですが、どちらを選ぶかによって最終的な資産の増え方は大きく変わってきます。
特に長い目で資産を拡大するためには、複利での運用は資産の増加幅を雪だるま式に拡大し、圧倒的に有利になります。
今回のブログでは、複利で運用した場合、単利運用と比べて一体どの程度の差が生じるのか、そして複利を味方につけると最強の戦力になる反面、敵に回した場合、こんなに恐ろしいことはないということも併せてお話ししたいと思います。

「単利」と「複利」の違い

まずは、単利と複利について、それぞれ簡単に説明しましょう。

単利とは「投資元本」に対して利子がつくことです。単利を計算式で表すと「元本×利回り」です。
つまり、常に同じ元本をもとに利子が決まります。
複利と違い、元本の額がそのまま維持されるため、利子も毎回同じ金額で積み重なっていきます。
単利とは元本の金額のまま運用することを言い、運用による収益は再投資されません。
単利で受け取れる金融商品の代表的なものは、個人向け国債です。
個人向け国債は、償還される額面によって、毎年２回、決まった利率で利子を受け取ることができます。
当たり前の計算ですし、あまり知られていないようですが、
お金が倍になるには何年かかるか、あるいは倍にしたい年数があって、その年数で資産を2倍にするには何％
の金利で運用すればいいかを求めるのに、「単利：100の法則」というものがあります。

お金が2倍になる期間（年）＝100÷金利（利回り）

例えば、年利3％で運用した場合には以下のような計算です。
【計算式】100÷3％＝33.333・・・年
つまり、お金が倍になるには33年以上かかるということになりますね。
相当の金利がないと、単利ではあまりお金が増えないようです。
反対に100を年数で割ると、その年数で資産を2倍にするには何％の金利で運用すればいいかがわかります。

一方で複利とは「投資元本と受け取った利子」に対して利子がつくことです。
計算式に表すと「(元本＋前年利子)×利回り」です。
元本に利子が組み込まれ、利子に対しても利子が発生するため、毎回受け取る利子の金額は年々増えていくことになります。
ですので、長期の運用においては、同じ利率ならば複利の方が圧倒的に大きく増えることになります。

資産運用なら「複利」が有利

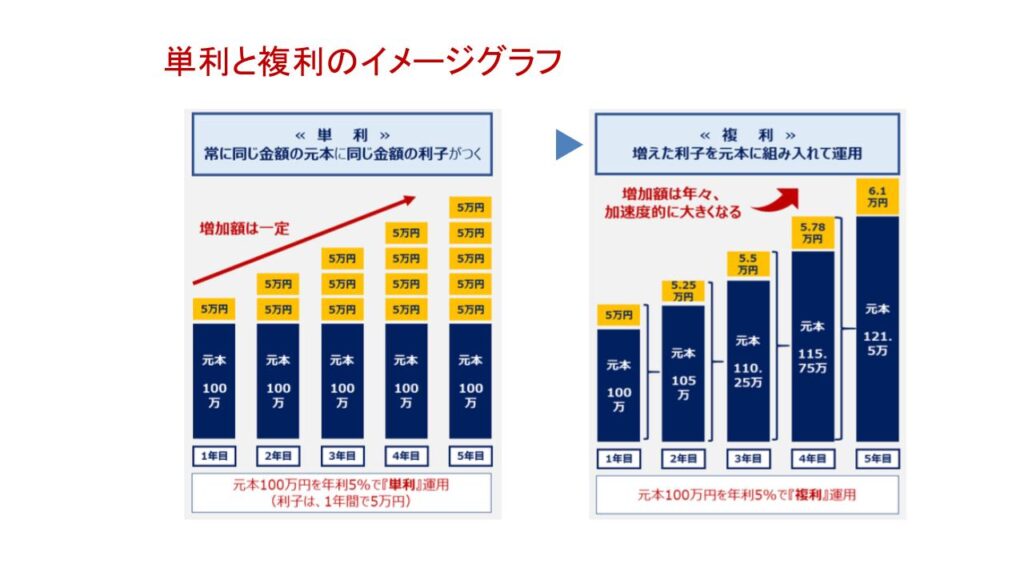
資産運用なら「複利」が有利「単利」と「複利」を、具体的な事例で比較してみましょう。
例えば、100万円を年利回り5％で5年運用したと仮定します。
税金などを考慮しなければ、単利で運用した場合、毎年5万円ずつ利子を受け取りますので、元本100万円と利子25万円(5万円×5年)で合計は125万円になります。一方、複利で運用した場合は、毎年の利子を元本に加えて運用します。
利子に対しても利子がつくため、5年運用した場合の元本の合計は127.6万円となり、単利よりも2.6万円多くなります。
このように同じ5年でも、元本が増え続ける複利運用の方が手元に多くの資産が残ります。
資産運用をするなら、複利の力を利用しない手はないという所以です。
しかし、5年で生じるこの程度の差なら、あの、相対性理論のアインシュタインさんが「宇宙で最も偉大な力」と驚嘆したとは思えませんね。

続けることでさらに高まる「複利効果」

資産運用をするなら複利が効果的なのですが、複利効果をさらにパワフルにする方法があります。
方法といっても、拍子抜けするほど簡単です。
複利での運用を長期にわたって継続する、ただそれだけのことです。

複利は長期投資と組み合わせることで、その効果が猛烈になります。

運用期間	単利	複利	利益の差
1年	1,050,000円	1,050,000円	0円
5年	1,250,000円	1,276,282円	26,282円
10年	1,500,000円	1,628,895円	128,895円
15年	1,750,000円	2,078,928円	328,928円
20年	2,000,000円	2,653,298円	653,298円
25年	2,250,000円	3,386,355円	1,136,355円
30年	2,500,000円	4,321,942円	1,821,942円

上表は、前項でシミュレーションした同じ条件(100万円を年利回り5％で運用)で、運用期間を30年まで伸ばしてシミュレーションしたものです。
単利の場合、資産を倍にするには20年が必要ですが、複利であれば15年目には資産を倍にできます。なんと、5年もの差がつくのです。
２０年と言わず、複利でさらに長期間運用すると、なんと30年後には元本の4倍以上もの資産を形成すること可能なのです。
こうなると、「複利は宇宙で最も偉大な力であり、人類最大の発明だ！」とアインシュタインがビックリしたのもわかります。
資産を大きく育てるなら、「複利で長期間運用すること」に限るというわけです。

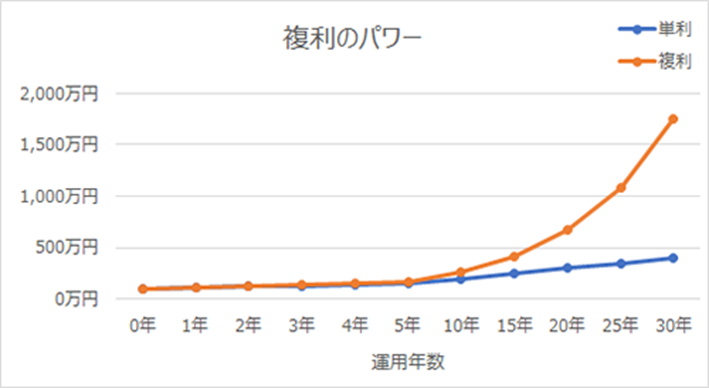
横軸が年数、縦軸が資産がどれだけ増えたか？というのを表すグラフにするとこうなります。
一目瞭然ですが、１０年で比べると運用利回りが１％で5％でも１０％でも、そんなに大きな差にはなりません。
しかしこれが２０年になると、差が相当大きくなり、それが３０年になると、全然違うと言っても良いほど大きな差になってしまいます。

雪だるま式にふえる複利

この、強烈極まりない複利のパワーは、よく「雪だるま式に増える」と表現されます。
雪の上で、雪玉を転がしたときのことをイメージしてみると、そう表現される理由がよくわかります。

雪玉＝元本
雪玉にくっついてくる雪＝複利

転がせば転がすほど、雪玉は大きくなっていきます。
このとき、最初に転がす雪玉が元本で、雪玉についてくる雪が複利の利息というイメージです。
これと同様のことが、複利の運用で起きるのです。
雪玉を転がし続ければ、そのうち、人の手ではとても転がせない大きさになりますが、お金はそういう制限がありません。長期の運用であればあるほど、際限なく収益が大きくなります。

ここで、今お話ししている「派手さ」とは対極の、預金について考えてみましょう。
預金には利息がつきますが、その利息も含めた金額が元本となり、次回の利息が計算されることで利息が膨らんでいく仕組みのことを指しますので、立派な「複利」です。
元来お金を預けることで利息が得られるという側面からは、預金・定期預金も立派な投資商品なのです。

事実、３５年ほど前。バブル期と呼ばれる頃には、定期預金でも10年で8％程度にもなっていた時期がありました。
この時代のお金のふえ方を、72の法則を用いて計算してみますと
【計算式】72÷8％＝9年
税金を計算に入れずに考えると、
定期預金したお金が9年で倍くらいになっていた時期も、実際にあったのです。
しかし今の時代、預金に「お金がふえる」イメージが全くないのは、ひとえに金利が低すぎるということによります。
現在の定期預金の金利がメガバンクで0.01％ですが、0.01％で運用したらどうなるかを計算してみましょう。

【計算式】72÷0.01％＝7200年

預けたお金を倍にするには、7200年もかかります。
我々の寿命のスパンを逸脱するにも程がありますよね。
我々が縄文時代に生きていて、銀行があってこの金利なら、現在まで７２００年間、ずっと預けていてようやく倍になりました、ということです。
いくらなんでも非現実的なシミュレーションなので、現実的に計算します。
2022年12月時点、預金で1年後の２０２３年１２月に1万円の利息を得ようとする場合は、定期預金でなんと5億円以上の預金額が必要。これは、紛れもない事実です。

いくら複利が偉大だとして、そしていくら複利で時間をかけたとしても、利回りがここまで低い場合には資産運用の成果は見込めません。
資産を効率よく増やしていくには、「複利」×「長期」に加え、一定の「利回り」を確保することが鍵となります。

資産を2倍にするために

金融の世界では有名ですが、「72の法則」というものがあります。
お金が2倍になるまでの金利と年数の関係を簡易的に求められる数式のことです。
2倍になる年数、金利を求める計算式は、それぞれ以下のとおりです。

お金が2倍になる年数 ≒ 72÷金利
お金が2倍になる金利 ≒ 年数÷72

年利3％で運用した場合、計算式は以下のようになります。
【計算式】72÷3％＝24年
つまり、24年でお金が2倍になるという結果です。

年利回り6％で運用した場合は、資産を2倍にするには72 ÷ 6％＝約12年。
あくまで概算ですが、およそ半分の年数で倍になるということがわかります。
そして、年利回りが高くなるに従って、資産が2倍になるために必要な年数は短くなっていきます。
反対に72を年数で割ると、その年数で資産を2倍にするには何％の金利で運用すればいいかがわかります。

また、この72の法則を使えば、インフレで物価が何倍になるかも計算することも可能です。
例えば、日銀は2％の物価上昇率を目標として量的緩和政策を行っています。
仮に物価目標が達成され、毎年平均して2％ずつ物価が上がった場合に何年後に物価が倍になっているのか計算してみましょう。

【計算式】72÷2％＝36年

もし日銀の物価目標の2％ずつ物価が上がり続けた場合、36年後には世の中の物価が倍になっていることがわかります。
つまり、36年後には現在1万円で買えるものは2万円になり、100万円のものは200万円になるということになります。

もちろん2％の物価上昇率が続いたときに定期預金の金利が現在の水準のまま、というのは現実的ではないか
もしれません。
しかし、金利3％ならば24年で2倍になるものが、0.01％だと7200年もかかる。
金利によってお金のふえ方にはとんでもなく大きな差が生じるということだけは間違いないことです。

72の法則のほかに、複利には「36の法則」というものもあります。
これは3.6％の金利で36年間複利運用すると、元本の約3.6倍になるという法則です。1000万円を3.6％で36年運用すれば3600万円になっているという計算です。

平均3.6％は債券などと組み合わせて、投資においては十分期待できる、安定的とも言える利回りです。
この現実的な運用利回りでも、複利の効果で36年間運用すると、このように大きく増やすこともできるということがわかります。

複利を敵にまわすと「ダース・ベイダー」級

ここまで、複利を味方につける重要性についてお話ししました。
投資で得た利益を再投資に回せば、元本にその再投資分を加えた金額に利息が雪だるま式についていくので、「複利」がお金をふやす「味方」になってくれるというものです。
さらに利回りを味方につけると、25歳から毎月2万数千円ずつ積み立てて利回り10％で運用したら、60歳で一
億円にもなります。

これほど猛烈なパワーを秘めた「複利」ですから、絶対に敵に回してはいけません。
複利というものは、いったん敵に回してしまうと、これほど怖いものはないのです。
スターウォーズでいえば、「ダース・ベイダー」クラスの恐ろしさだと思ってください。

クレジットカードは持っているとかっこいいと思うかもしれませんが、使い方によっては家計を圧迫することになる可能性が大いにあります。

中でもほとんどのクレジットカードについているキャッシング機能やリボ払いは、もっとも危険なものです。頻繁にCMで見かける「カードローン」もそうです。「ぱっとピッとプロミス」「愛がいちばんアイフル」「はじめてのアコム」全て破壊的です。
コンビニやATMで気軽にお金が借りられて一見便利ですが、これが大きな間違いなのです。
理由は、年率15%～18％という高金利が一般的だからです。全体に手を出してはいけません！

金利18.0%の場合、「72の法則」にこれを当てはめると、
72÷18（%）≒4（年）
なんと、約4年で借りたお金（借金）が2倍にもなってしまいます。

元のお金が100万円であれば、元金＋利息の総額が4年で200万円になる、ということです。
うっかり軽い気持ちでキャッシングやリボ払いやカードローンをしてしまうと、その瞬間、最強の複利を敵に回してしまうのです。大きな利息で返済総額がふくらみ続け、気がつけばとても返せない額になってしまう。「ナニワ金融道」で銀ちゃんにお世話になる人は、冗談抜きにほぼこのパターンです。

「ふやす」というサブテーマの１回目に、あえて「複利」というテーマを選びましたが、今回のブログは、ためになりましたでしょうか？

資産運用や投資の本で、必ず主張されていることは、「資産運用は早く始めるに越したことはないですよ」と言うことです。

その理由が、よくお分かりいただけたと思いますが、いかがでしょう。
このブログの中で「ふやす」というサブテーマを連載するのは、専門家のような知識レベルではなくても、今すぐに投資を始められるだけの実践的な知識を身につけていただくためです。
このブログを、時間のある時に続けてお読みいただければ、
多くの人が投資をして陥る失敗をしないための最低限の知識がしっかり身につきますし、投資を成功させるために十分な秘訣を知ることができると自負しつつ、しっかり連載して行きたいと考えています。

「ふやす」というサブテーマの２回目は、お金自体がどれだけの働き者であるか、どれほど稼ぐ能力を持っているか、自分自身でどれだけふえることができるのか、ということについて書きたいと思います。
乞うご期待！